At first, we sample  in the
in the  (
( is odd) equidistant points around
is odd) equidistant points around  : [ f_k = f(x_k),\: x_k = x^+kh,\: k=-\frac{N-1}{2},\dots,\frac{N-1}{2}
: [ f_k = f(x_k),\: x_k = x^+kh,\: k=-\frac{N-1}{2},\dots,\frac{N-1}{2}
]
where  is some step.
is some step.
Then we interpolate points  by polynomial
by polynomial
(1)
Its coefficients
(2)
Here are references to existing equations: (1), (2).
Here is reference to non-existing equation (??).
一、 随堂练习
- 定义域计算
- 已知函数
的定义域为
,则函数
的定义域为多少?
- 设函数
的定义域为
,求
的定义域。
- 已知函数
,则
的定义域是( )A.
B.
C.
D.
- 已知函数
- 反函数计算
- 计算下列函数的反函数:(1)
(2)
- 计算下列函数的反函数:(1)
- 复合函数分解
- 分解下列复合函数:(1)
(2)
- 分解下列复合函数:(1)
- 函数的奇偶性
- 函数
是( )A. 偶函数 B. 奇函数 C. 非奇非偶函数 D. 无法判断
- 判断下列函数的奇偶性:(1)
(2)
- 函数
二、【练好题】基础篇
- 已知函数
的定义域为
,则下列函数定义域是
的函数为( )A.
B.
C.
D.
- 已知函数
的定义域为
,则函数
的定义域是( )A.
B.
C.
D.
- 函数
的定义域为 ______。
- 函数
的定义域为 ______。
- 函数
的定义域为 ______。
- 计算下列函数的反函数:(1)
(2)
- 判断下列函数的奇偶性:(1)
(2)
(3)
(4)
三、【练好题】进阶篇
- 已知函数
的定义域为
,则函数
定义域为( )A.
B.
C.
D.
- 函数
的定义域为 ______。
- 函数
的定义域为 ______。
- 函数
的定义域为 ______。
- 已知函数
的定义域为
,则函数
的定义域为 ______。
- 计算下列函数的反函数:(1)
(2)
(3)
- 判断下列函数的奇偶性:(1)
(2)
(3)
(4)
(5)
第二节 极限
一、 随堂练习
1. 代值法与四则运算
- 计算极限
- 计算极限
- 计算极限
- 计算极限
- 计算极限
2. 因式分解法
(注:根据上下文推测为立方根)
3. 无穷因子消去法(抓大头)
- 设
,则
___,
___。
- 计算极限
- 计算极限
(注:题目原文可能有误,按标准题型整理)
- 计算极限
- 计算极限
4. 无穷小量与无穷大量
- 计算极限
- 计算极限
- 计算极限
(注:可能涉及无穷大判断)
- 计算极限
- 计算极限
- 计算极限
5. 极限存在准则与两个重要极限
- 函数
,求
是多少?
- 已知函数
在
处极限存在,则
___。
- 已知极限
,则
___。
___。
6. 无穷小量的比较与替换
- 当
时,
与
相比是( )A. 高阶无穷小 B. 低阶无穷小 C. 等价无穷小 D. 同阶非等价无穷小
- 当
时,函数
与
是等价无穷小,则常数
的值为( )A. -1 B. 1 C. -2 D. 2
- 已知极限
,则常数
___。(注:根据题意补充了分母形式)
- 求极限
(注:原文可能为
或类似,直接计算为0)
- 下列极限存在的是( )A.
B.
C.
D.
- 已知当
时,
与
是等价无穷小,则
___。
- 计算极限
- 计算极限
- 计算极限
二、【练好题】基础篇
___。
- 当
时,
与
相比是( )A. 高阶无穷小 B. 低阶无穷小 C. 等价无穷小 D. 同阶非等价无穷小
- 当
时,与
等价的无穷小量是( )A.
B.
C.
D.
- 已知极限
,则常数
的值为( )A. -1 B. 1 C. 2 D. -2
___。
___。
___。
- 已知
,则
___,
___。
- 当
时,
与
是等价无穷小量,则
___。
- 已知函数
在
处极限存在,则
___。
- 计算下列极限:(1)
(3)
(4)
(5)
(6)
(7)
(8)
(9)
(10)
(11)
(12)
(13)
(注:原文模糊,推测为sin/sin结构)(14)
(15)
(16)
- 已知函数
,计算
与
,并求
。
三、【练好题】进阶篇
- 当
时,
的极限为( )A. -2 B. 1 C. 2 D.
- 计算极限
___。
- 计算极限
___。
- 当
时,函数
与函数
(注:原文模糊,推测为某等价无穷小)等价,则
___。
- 已知极限
,则
___。
- 已知函数
,计算
与
,并求
。
- 计算极限:(1)
(2)
(3)
(4)
(5)
(6)
(7)
(8)
(9)
(10)
(11)
(12)
(13)
(14)
第三节 连续
一、 随堂练习
- 设函数
在
处连续,则
的值为 ___。
- 设函数
,判断其在
处是否连续。
是函数
的( )A. 连续点 B. 可去间断点 C. 跳跃间断点 D. 无穷间断点
- 点
是函数
的( )A. 连续点 B. 可去间断点 C. 跳跃间断点 D. 无穷间断点
- 点
是函数
的( )A. 连续点 B. 可去间断点 C. 跳跃间断点 D. 无穷间断点
二、【练好题】基础篇
- 点
在函数
中是( )A. 有定义 B. 极限不存在 C. 连续 D. 极限存在
- 函数
的间断点个数为( )A. 1 B. 0 C. 2 D. 3
- 点
在函数
中是( )A. 可去间断点 B. 无穷间断点 C. 连续点 D. 跳跃间断点
在函数
中是( )A. 可去间断点 B. 跳跃间断点 C. 连续点 D. 振荡间断点
- 对于函数
,以下结论正确的是( )A.
是第一类间断点,
是第二类间断点B.
是第二类间断点,
是第一类间断点C.
是第一类间断点,
是第一类间断点D.
是第二类间断点,
是第二类间断点
- 设
,则
是
的( )A. 无穷间断点 B. 振荡间断点 C. 跳跃间断点 D. 连续点
三、【练好题】进阶篇
- 点
为函数
的( )A. 可去间断点 B. 无穷间断点 C. 连续点 D. 跳跃间断点
- 函数
的间断点个数为( )A. 1 B. 0 C. 2 D. 3
,则
是
的( )A. 可去间断点 B. 无穷间断点 C. 第二类间断点 D. 跳跃间断点
- 已知函数
在
处连续,则常数
___。
- 已知
在
处连续,则常数
___。

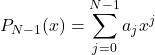
 ,求
,求  在
在  在
在  在
在  ,判断其在
,判断其在  ,则
,则  在
在  在
在 




评论0